RECENT PUBLICATIONS

Deviations Due To Non-Newtonian Influences Within a Miniature Viscous Disk Pump (P. M. Ligrani, H. Jiang, B. Lund, and J. S. Jin), ASME Transactions-Journal of Fluids Engineering, Vol. 135, No. 3, pp. 031205-1 to 031205-12, March 2013. DOWNLOAD COPY OF PAPER

Elastic Turbulence Effects on the Performance of a Miniature Viscous Disk Pump (B. Lund, M. Brown, M. Jennerjohn, P. M. Ligrani, and A. Fatemi), Paper Number IMECE2015-52596, IMECE 2015, International Mechanical Engineering Congress and Exposition, Houston, Texas, USA, November 13-19, 2015.

Onset and Transition to Elastic Turbulence:  Effects of Rheological Property Variations For Polyacrylamide-Water Solutions (B. Lund, P. M. Ligrani, and A. Fatemi), Invited Paper, 20^th International Colloquium Tribology – Industrial and Automotive Lubrication, Stuttgart / Ostfildern, Germany, 12-14 January 2016.

Development and Control of Elastic Turbulence Within a Micro-Scale Viscous Disk Pump (B. Lund, P. M. Ligrani, and M. Brown), Advances and Applications in Fluid Mechanics Journal, Vo. 19, No. 3, pp. 517-539, August 2016.

Miniature Viscous Disk Pump: Performance Variations From Non-Newtonian Elastic Turbulence (P. M. Ligrani, B. Lund, and A. Fatemi), ASME Transactions-Journal of Fluids Engineering, Vol. 139, No. 2, pp.021104-01 to 021104-10, February 2017. DOWNLOAD COPY OF PAPER

Elastic Turbulence Influences and Convective Heat Transfer Within a Miniature Viscous Disk Pump (D. Copeland, C. Ren, M. Su, and P. M. Ligrani), International Journal of Heat and Mass Transfer, Vol. 108, Part B, pp. 1764-1774, May 2017.

Heat Transfer Enhancements From Elastic Turbulence Using Sucrose-Based Polymer Solutions (P. M. Ligrani, D. Copeland, C. Ren, M. Su, and M. Suzuki), AIAA Journal of Thermophysics and Heat Transfer, Vol. 32, No. 1, pp. 51-60, January 2018.

Heat Transfer Enhancements From Elastic Turbulence Within Rotating Couette Flow Using Sucrose-Based Polymer Solutions (P. M. Ligrani), Plenary Lecture, ICAYS – 2018 International Conference in Aerospace for Young Scientists, School of Aeronautic Science and Engineering (ASE), Beihang University, Beijing, P. R. China, September 15-16, 2018.

Thermal Transport of Viscoelastic Fluids Within Rotating Couette Flows (P. M. Ligrani, M. Su, A. Pippert, and R. A. Handler), AIAA Journal of Thermophysics and Heat Transfer, Vol. 34, No. 1, pp. 121-133, January 2020.

Vortex Generation in a Finitely Extensible Nonlinear Elastic Peterlin Fluid Initially at Rest (R. A. Handler, E. Blaisten-Barojas, P. M. Ligrani, P. Dong, and M. Paige), Engineering Reports, Vol. 2, No. 3, pp. 1-17, March 2020.

HEAT TRANSFER ENHANCEMENTS FROM ELASTIC TURBULENCE USING SUCROSE-BASED POLYMER SOLUTIONS

The influences of elastic turbulence on convective heat transfer, within a C-shaped passage of a viscous disk pump, are experimentally determined using viscoelastic fluids. Different concentrations of polyacrylamide in 65 percent sucrose solutions are used, along with solutions with 65 percent sucrose only, as different magnitudes of shear stress and strain rate are imposed upon the flow field. Transition and development of elastic turbulence are characterized, along with convective heat transfer enhancements. The resulting increased levels of mixing, transport, and diffusion from elastic turbulence give convective heat transfer coefficient enhancements which are as large as 240 percent, relative to the Newtonian fluids at the same shear rate, rotation speed, flow passage height, and flow temperature. Variations of spectra of static temperature fluctuations, and mean-square magnitudes of fluctuating static temperature provide evidence of increased flow irregularities and unsteadiness (relative to Newtonian solution flows), which result from elastic turbulence induced polymer twisting, convolutions, and interactions. Such observed enhancements are shown to not be due to increased viscosity values alone, nor to centrifugal instabilities associated with streamline curvature, since Dean numbers are not large enough to allow development of the associated centrifugal-instability induced secondary flows.

Nomenclature

Greek Symbols Nomenclature

 I. Introduction

Elastic turbulence has recently emerged as an innovative approach to increase convective heat transfer in microscopic and millimeter-scale applications. Elastic turbulence is characterized by an increase in mixing and secondary flows due to the stretching and twisting of polymers in a viscoelastic fluid. The onset of elastic turbulence occurs due to interactions between polymers in the form of coil stretch transition [1]. Because these effects are observed at very low Reynolds numbers, elastic turbulence offers a means to enhance convective heat transfer in microscopic and millimeter-scale applications, where other means of increasing heat transfer are a challenge to implement. Elastic turbulence is induced by adding polyacrylamide to Newtonian solvents that then undergo shear stresses in curvilinear geometries. As a result, mixing and chaotic motions associated with the onset of elastic turbulence are often observed at low Reynolds numbers with values less than 1.

Elastic turbulence phenomena occur when elastic polymer solutions within liquids are excited by a mechanical stress, and then exhibit highly non-linear and non-Newtonian behavior. The mechanical stresses act on the polymers within the flow stretching the polymers, causing a secondary flow. This secondary flow acts back on the polymers within the solution and stretches them, resulting in flow transition from laminar to turbulent flow. As such, the rheological properties of polymer solutions are essential ingredients for the onset and development of elastic turbulence. This is because elastic turbulence phenomena occur when polymer extensibility and deformation lead to a sharp growth in the local elastic stress, a sequence of events referred to as the Weissenberg instability. This instability occurs when the Weissenberg number is greater than an onset value which depends upon experimental configuration, shear rate, polymer type, polymer concentration, and other parameters. The associated stress growth gives polymer stretching, resulting in highly non-linear and non-Newtonian behavior, increased local secondary flows, increased mixing, and chaotic fluid motions [1]. As a result, the polymer flows transition from laminar to turbulent flow through elasticity (rather than inertia) at very low Reynolds numbers.

Several studies consider transition and diffusion associated with elastic instabilities and elastic turbulence at different experimental conditions. For example, Nashie et al. [2] numerically predict diffusion and flow behavior within a circular body of revolution. Spatial chaos due to non-linear dynamics is observed, leading to increased mixing and diffusion. Berti and Boffetta [3] and Berti et al. [4] investigate elastic turbulence using two-dimensional Kolmogorov flow. Their results show that viscoelastic flows demonstrate increased mixing features and complexity with very small inertial non-linearity. Schiamberg et al. [5] report experimentally measured secondary flows, which often arise in viscoelastic flows between parallel plates, with negligible inertial effects. Li et al. [6] induce chaotic fluid motions in micro-channels with viscoelastic surfactant solutions at very low Reynold numbers. The resulting viscoelastic flows, within different flow configurations, exhibit turbulent characteristics as elastic turbulence develops, which promotes flow mixing and chaos over relatively large spatial regions.

Hartnett and Kostic [7] and Hartnett [8] investigate heat transfer within viscoelastic aqueous polymer solutions in channel flows. Results indicate that viscoelastic fluids exhibit enhanced heat transfer coefficients, which are attributed to secondary motions associated with local and global normal stress variations. Abed et al. [9] and Whalley et al. [10] present experimental results for a serpentine channel to study convective heat transfer enhancements due to elastic turbulence. Results show that convective heat transfer magnitudes are enhanced by as much as 200 to 380 percent, for solutions with relatively low concentrations of polymers and relatively high concentrations of sucrose, compared to results for Newtonian solutions. Traore et al. [11] describe increases in heat transfer efficiency within von Karman flows due to elastic turbulence. Results illustrate efficient heat transport at low Reynolds numbers. Numerical investigations are described by Zhang et al. [12,13], which address connections between elastic turbulence, and enhancements of local flow mixing.

Within the present investigation, a miniature viscous disk pump (VDP) [14,15] is utilized for experimental study of the effects of elastic turbulence with heat transfer. The experiment is undertaken using a viscoelastic solution with polyacrylamide, and 65 percent sucrose. Used as a basis of comparison are increased-viscosity Newtonian fluids, which generally do not change viscosity as shear rate varies [16]. Such solutions are created with sucrose, but without any type of added polymer. Comparisons between the two types of fluids are generally undertaken at the same rotation speed, shear rate, flow passage height, and inlet temperature. Such Boger fluids are dilute polymer solutions, characterized by constant viscosity that is independent of shear rate [16]. With such comparisons, results associated with elastic turbulence flows show distinctive different characteristics. With the present VDP arrangement, the flow passage height is 640 μm, and rotation speed ranges from 10.47 to 209.4 radians/sec. Heat transfer measurements are based upon energy balance considerations, which utilize the mixed-mean temperature at the inlet and outlet of the viscous disk pump passage. The overall heat transfer rate is determined based upon a constant surface temperature thermal boundary condition, and upon a log-mean-temperature difference approach. The thermal boundary condition at the side walls and bottom wall of the VDP passage is constant temperature, whereas the rotating disk is adiabatic. Included are flow visualization results, variations of shear stress, strain rate, and viscosity, pressure rise data, spatially-averaged heat transfer coefficients, spatially-averaged Nusselt numbers, and spectral analysis of the temperature fluctuations. Overall aims include presentation of data which illustrate enhanced thermal transport and convective heat transfer rates due to elastic turbulence. As such, the present investigation provides new insight into the mechanisms of elastic turbulence, and the conditions at which it occurs, as well as the effects on convective heat transfer, within an environment which has never before been employed for this purpose.

II. Viscous Disc Pump

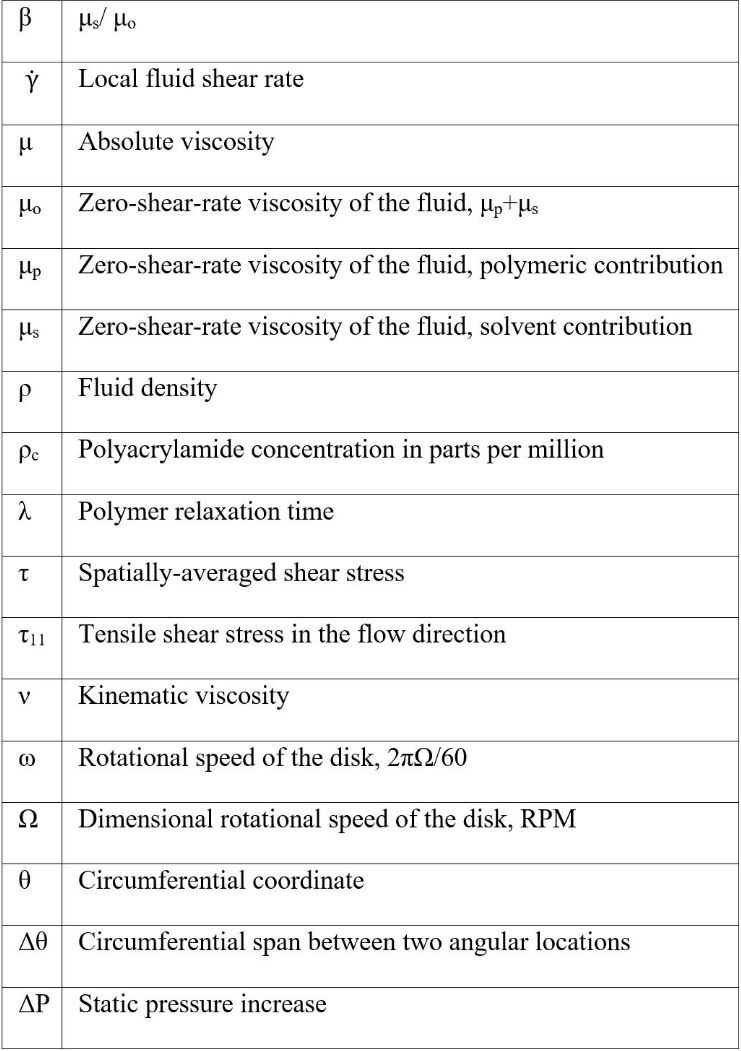
The viscous disk pump or VDP experimental apparatus is composed of a spinning disk and a C-shaped channel with a fluid inlet port and a fluid outlet port, located at the two ends of the C-shaped channel. Details regarding these different items are provided by Ligrani et al. [14], and by Blanchard et al. [15]. The overall arrangement, coordinate system for the flow passage, and dimensions are schematically shown in Fig. 1. Within this figure, the shaded region of the pump chamber is used for the flow analysis. The z coordinate is directed normal to the surface, and measured from the stationary flat bottom surface of the flow passage. The flow passage height for the present investigation is 640 μm. Rotation speeds range from 10.47 to 209.4 radians/sec. As the disk rotates, its edges create a seal to minimize the leakage of working fluid by contacting the fluid chamber wall. Rotating Couette-type flow is thus induced in the fluid chamber between the rotating disk and the stationary bottom of the channel. The work done on the fluid by the rotating disk then leads to a circumferential pressure gradient within the C-shaped channel, such that static pressure increases with streamwise development. The VDP with a C-shaped channel is thus employed because magnitudes of shear rate imposed on the flow are readily selected by setting disk rotational speed and the gap height of the flow passage.

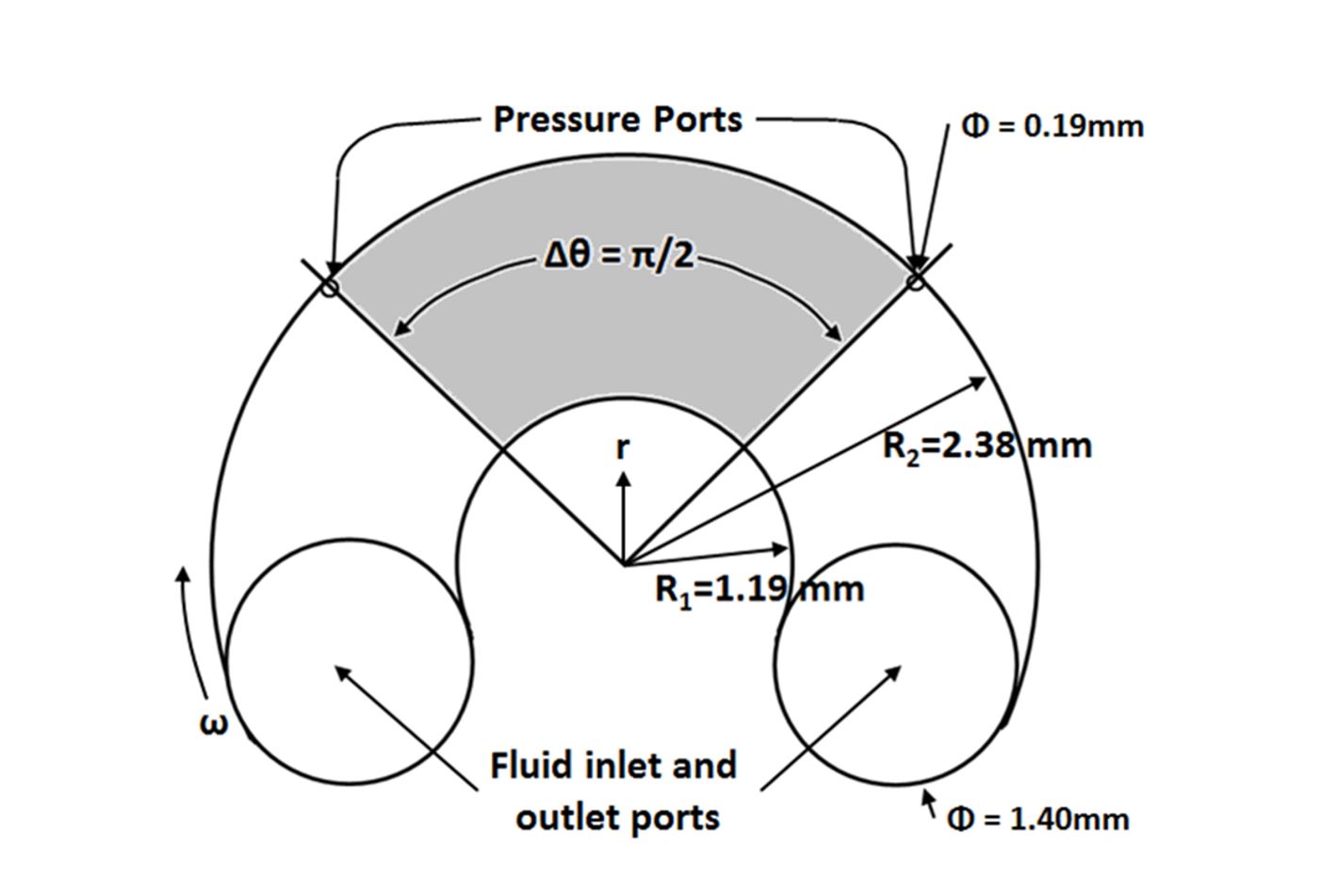
Figure 1. Configuration of the single-disk viscous pump, including coordinate system

III. Polymer Solution Preparation

Four different solutions are utilized with four different polymer concentrations: 0 ppm, 80 ppm, 100 ppm, and 150 ppm, where ppm refers to parts per million. As such, the 0 ppm arrangement is utilized with a 65 % sugar solution (without added polymers) to create a Newtonian solution with an approximately constant viscosity that is independent of shear rate [16]. The viscoelastic solutions are then prepared by adding polyacrylamide powder into the sucrose solution. When each solution is prepared, the appropriate polymer concentration (as quantified using PAAm) is employed, along with 1 % NaCl, and 65 % sucrose. The procedure for mixing the stock solution is adopted from Abed et al. [9]. For example, to mix a 80 ppm solution, 0.048g of PAAm (Polyacrylamide, M_w = 18,000,000 Dalton, Polysciences Inc.) powder, 6 g of NaCl, and 390 g sucrose are dissolved in 204 g DI water, as the solution is gently combined for approximately 4 hours within a commercial mixer, with a propeller operating at moderate speed.

Polymer mixture rheological data are obtained using a commercial Anton Paar Rheometer MCR 302. These data are employed to provide information regarding absolute viscosity properties of the different fluids which are used for testing, as viscosity varies with shear rate and shear stress.

IV. Flow Visualization Apparatus and Procedures

The disk pump is powered by an externally mounted Maxon EC32 #118890 motor. The motor has a 48V winding, a power rating of 80W, a maximum speed of 25,000 RPM, and a stall torque of 0.353 Nm. The motor is controlled by a Maxon ESCON 50/5 #409510 motor controller connected to an Advanced Motion Controls model PS2X3W48 power supply. The power supply has a DC supply voltage of 48V, a peak current of 12 amperes, and a continuous current rating of 6 amps. The motor controller maintains a constant speed through a closed control loop and a Maxon HEDL 55 Encoder #110514. The speed and direction of the motor are controlled by regulating voltage to the analog and digital I/O channels on the motor controller using LabVIEW 32-bit software, version 10.0.1, and a Nation Instruments USB6003 data acquisition board. The rotational speed measurement system is calibrated using a timing light. To measure the time-averaged fluid flow rate, the combination of a valve, timer, and Adam PGL2002 measuring scale are employed. The pump assembly is mounted to the base of a linear slide.  The brushless motor and disk shaft are also mounted to the shuttle of the linear slide. The disk shaft is supported with two bearings, and the distal end of the disk shaft connects to the motor shaft.  Elastic bands are employed to exert a constant force on the shuttle in the direction of the pump chamber to keep the disk surface flush against the bottom of the pump housing.  An alignment fixture is used to mount the pump housing and pump chamber, such that the axis of the disk aligns with the center point of the pump chamber radius. The pump assembly is placed on a level surface to ensure that there are no height differences between the flow inlet and outlet ports or between the two pressure ports. After assembling the disk, disk shaft, and pump chamber, the fluid inlet and outlet tubing are press-fit into the top of the pump housing. Before the test start, the tubing, and pump housing are filled with the working fluid. Syringes are subsequently used to remove any air from the liquid which is contained within the system.

The pump housing block is made from optically clear acrylic. Note that the flow passages turn ninety degrees toward the sides of the block, at a location which is approximately 12 to 14 mm beneath the surface of the channel, so that visualization views are not obstructed. The acrylic is polished using NOVUS plastic polish to remove any tooling marks and blemishes. An LED (light emitting diode) flashlight on a gooseneck clamp is directed at the Delrin disk to provide backlighting in the channel. A Point Gray CMLN-13S2C-CS USB camera, with a 25 mm lens, records images of the channel at a rate of 15 frames per second. The images are saved as 8-bit indexed .bmp image files and assembled into videos using the ffmpeg codec software. To provide contrast in the channel, Kingscote fluorescent FWT red tracer dye is injected into the channel with a New Era Pump Systems NE-1000 syringe pump at rates ranging from 0.001 to 0.065 milliliters per minute. Pure dye with 100 percent concentration is employed for this purpose. The syringe is 28.58 mm in diameter and is connected through tubing to a needle positioned in the inlet flow passage. Throughout testing, the inlet reservoir is maintained at a constant level, which is aligned with the outlet tubing, to minimize variations due to hydrostatic pressure and gravity.

V. Heat Transfer and Fluctuating Temperature Apparatus and Procedures

Within the present study, the VDP is employed for measurement of spatially-averaged heat transfer coefficients and Nusselt numbers over the entire flow passage surface area, as well as measurement of the fluctuating temperature within the exit part of the flow passage. To accomplish this task, fluid temperature is measured at the inlet and outlet of the flow passage using Omega 5TC-TT-T-40-72 fine-wire copper-constantan (Type T) thermocouples. Inlet temperature is measured using one thermocouple located at the central part of the beaker which supplies the working fluid. This temperature is representative of the mixed mean temperature at the inlet of the VDP flow passage, because of the absence of any temperature gradients within the apparatus up to and upstream of that location. In general, the inlet temperature is constant at approximately 22 ºC, which is the same as room temperature. The temperature of the fluid at the outlet of the VDP is measured using the apparatus which is shown in Fig. 2. The associated thermocouple at the outlet is fixed with glue and dried for 24 hours to insure that it is immobile as testing is underway. Because of the mixing which takes place within the flow, and the transient means whereby the fluid is displaced from the inlet to the outlet of the VDP flow passage, this measured temperature is representative of the fluid mixed mean temperature at the exit of the VDP flow passage.

Figure 2. (a) Dimensions and (b) photograph of the thermocouple located at the flow passage outlet.

In order to determine time-averaged magnitudes of the mean-squared temperature fluctuation, instantaneous flow temperature variations are recorded using the inlet and outlet thermocouples over a period of 90 s at a frequency of 100 Hz, after flow within the VDP reaches a steady-state operating condition. The mean square of fluctuating temperature, relative to the time-averaged temperature, is then determined using EXCEL software. To determine power spectra of fluctuating temperature, the MATLAB software code is employed. This code utilizes a Fast Fourier Transform (FFT) applied to instantaneous time-varying temperature data. To reduce levels of background, “white” noise, a Savitzky-Golay filter is applied. The frequency response of the thermocouple junction for these measurements is estimated to be approximately 0.12 to 0.16 milliseconds.

As temperature data are acquired, thermocouple voltages are read sequentially using a National Instruments NI 9213 thermocouple input card mounted within a National Instruments NI cDAQ-9188 chassis, connected to the computer workstation. These terminals relay the information to a Dell Precision T1700 computer. The voltage outputs from this unit are acquired by the computer through its USB port, using LABVIEW 11.0 software. With the procedures employed, the thermocouples have a measurement accuracy of 0.05ºC to 0.10ºC, and are calibrated in the range 20ºC to 44ºC using an HCTB-3020 Omega Thermo-Regulator.

VI. Analytic Determination of Nusselt Numbers and Heat Transfer Coefficients

Heat transfer measurements are based upon energy balance considerations, which utilize the mixed-mean temperature at the inlet and outlet of the viscous disk pump flow passage. The overall heat transfer rate is determined based upon a constant surface temperature thermal boundary condition, and upon a log-mean-temperature difference approach. The thermal boundary condition at the bottom surface and side walls of the VDP passage is constant temperature, whereas the rotating disk is adiabatic. This constant surface temperature boundary condition is achieved within the VDP for the bottom flow passage surface and the side walls because they are made of stainless aluminum with relatively high magnitude of thermal conductivity (k_Al=205 W/mK). The rotating disk is machined from PEEK plastic with a thermal conductivity of 0.252 W/(m·K), to minimize heat loss from the flow passage, and to minimize shape variations which may occur as heat transfer tests are underway.

With these considerations in mind, the bottom and side walls of VDP flow passage are maintained at constant temperature, Ts, and the rotating disk which is adjacent to the working fluid is adiabatic, such that q_disk=0. The log-mean-temperature difference equation is then applied between the outlet and the inlet of the VDP flow passage, as follows

Note that both temperature and velocity fields are expected to be fully-developed at a very short streamwise distance downstream of the fluid inlet port. Within Eqn. (1), L is the characteristic length which is given by

P is then the channel perimeter, and D is the portion of the perimeter where the constant temperature boundary condition is applied. These quantities are determined from the equations given by

The total heat flux into the VDP flow passage is then expressed using

where T_in and T_out are inlet and outlet flow passage mixed mean temperatures, respectively. Rearranging Eqn. (5) then gives

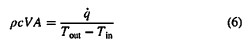
After further rearrangement, the overall VDP passage heat transfer coefficient is then determined using

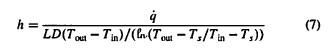
The overall Nussult number is then given by

where h is the overall flow passage heat transfer coefficient.

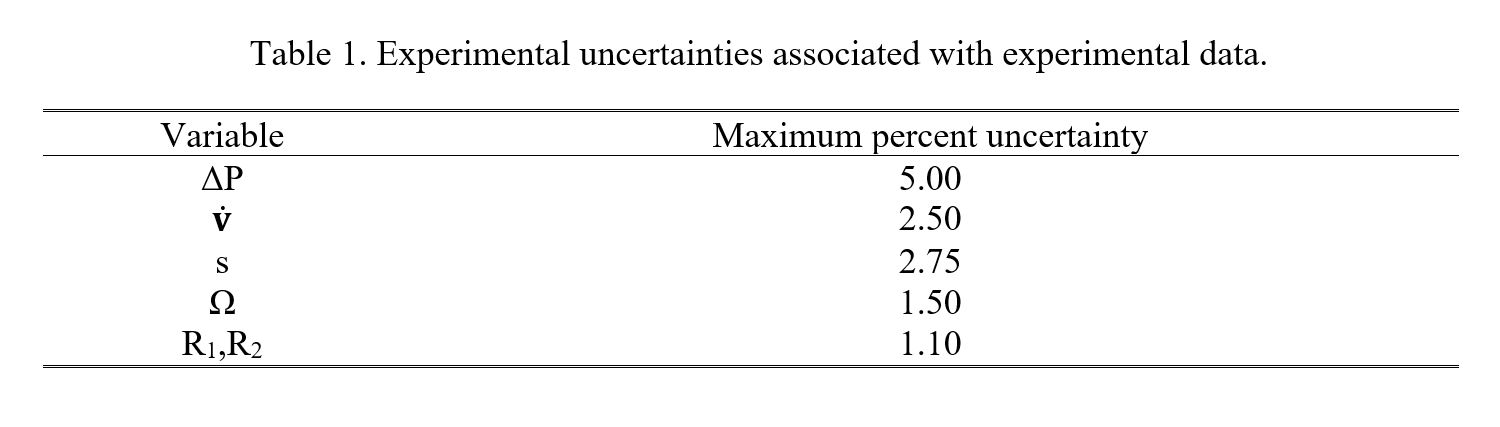
VII. Experimental Uncertainty Magnitudes

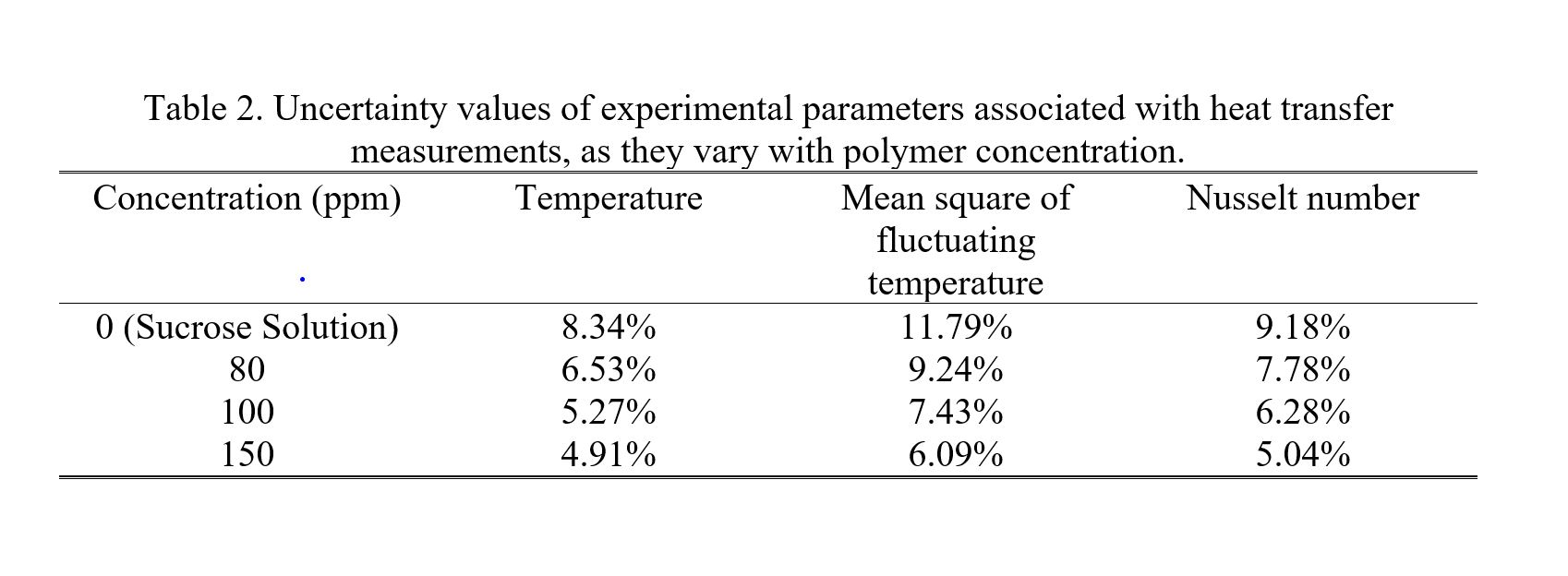
Experimental uncertainty magnitudes associated with measured quantities are provided in Table 1. Uncertainty magnitudes for different heat transfer related quantities are then provided in Table 2. Within this latter table, values are given for the sucrose-based Boger fluid, as well as for solutions with three different polymer concentrations.

VIII. Experimental Results and Discussion

A. Experimental Conditions

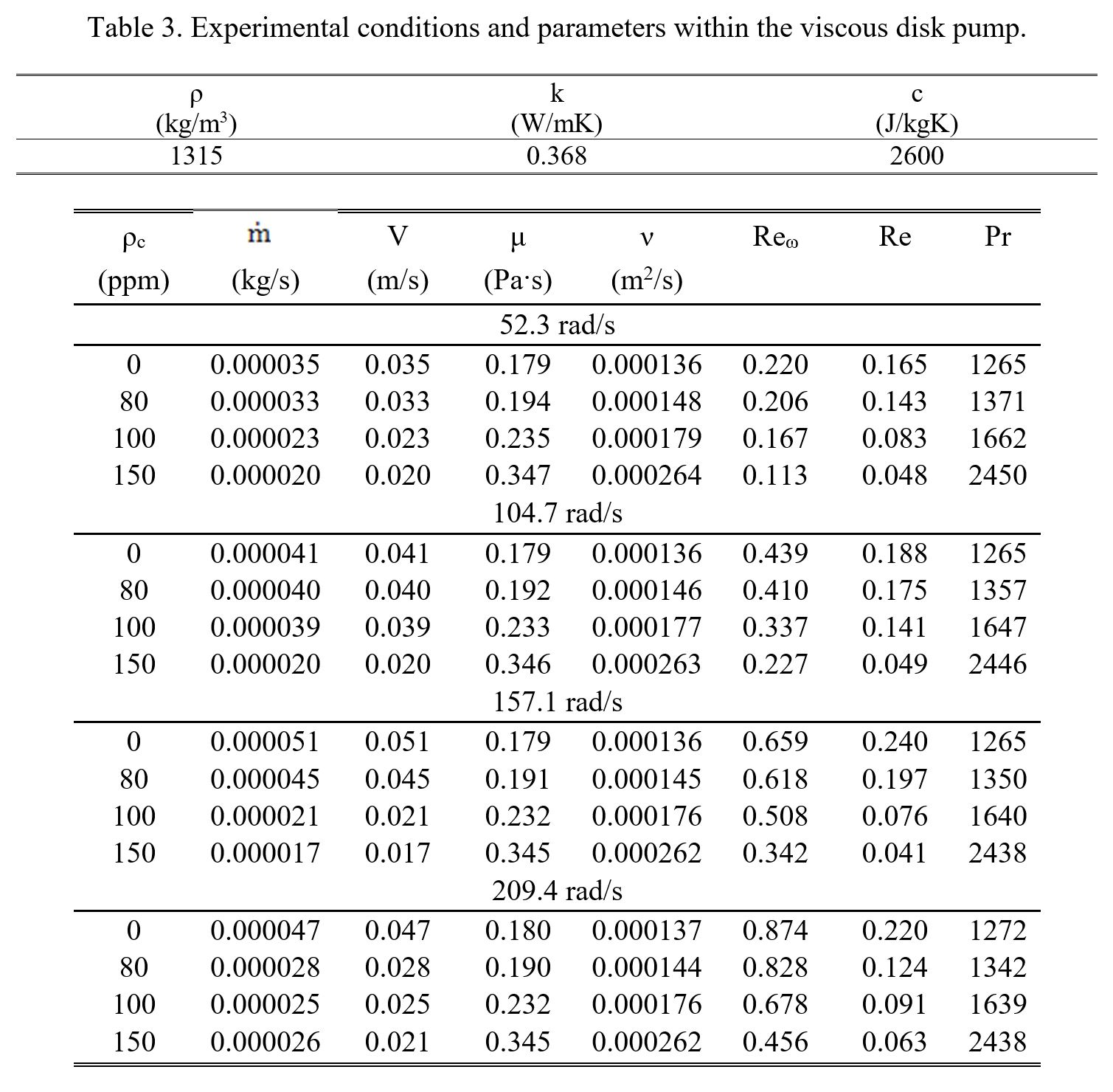
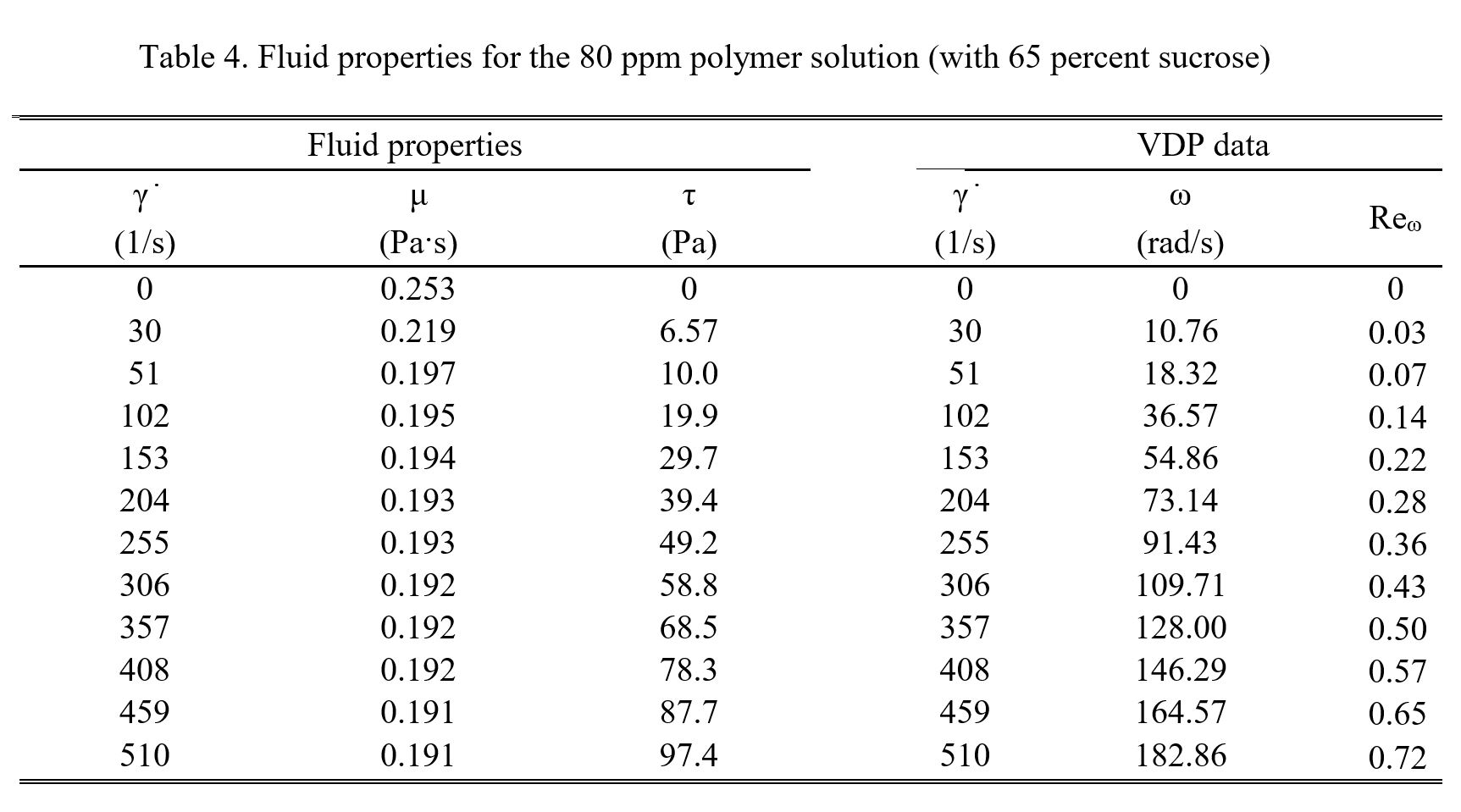
Table 3 provides information on experimental conditions and parameters which are employed within the viscous disk pump. Included are values of fluid molecular thermal conductivity, specific heat, and static density. Fluid flow mass flow rate, absolute viscosity, kinematic viscosity, molecular Prandtl number, Reynolds number, and flow passage average velocity are then provided for different disk rotational speeds, and different polymer concentrations. Note that some of the property values presented within Table 3 are from Abed et al. [9]. Table 4 then provides data obtained using the Anton Paar Rheometer MCR 302, including magnitudes of absolute fluid viscosity, as it varies with shear rate, and shear stress. Associated values of shear rate and rotational speed, which are associated with the viscous disk pump, are then included in this latter table for comparison. From Table 3, Reynolds numbers, based upon flow passage gap height and spatially-averaged velocity, range from 0.03 to 0.24, and Reynolds numbers, based upon flow passage gap height and rotation speed at the flow passage centerline, range from 0.11 to 0.87.

B. Variations of Viscosity With Shear Rate

Figure 3 shows variations of viscosity with shear rate, for shear rates up to 500 1/s. These data are provided for Newtonian fluids, which are sucrose solvents. The data in Figs. 3 and 4 are obtained using the Anton Paar Rheometer at fluid temperatures from 20^oC  to 40^oC, with data from Abed et al. [9] also included. Within Fig. 3, the viscosity is approximately invariant with shear rate for each fluid temperature. Here, for a given shear rate magnitude, the highest absolute viscosity is associated with the lowest fluid temperature.

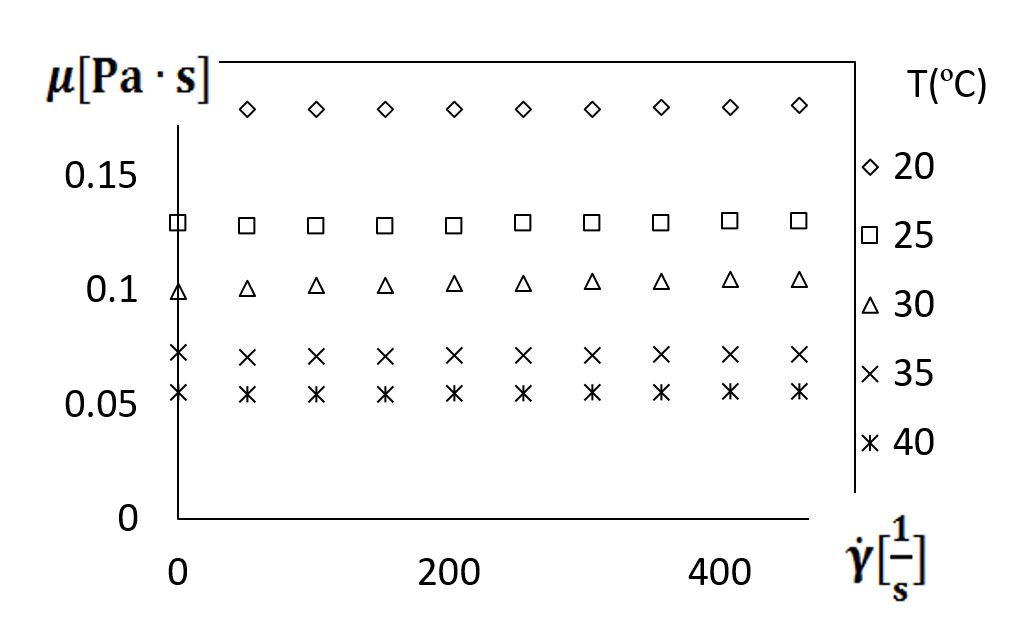
Figure 3. Viscosity variations with shear rate for sucrose solutions (Boger solution fluids), for different fluid temperatures.

Comparing these results to the data within Fig. 4 shows that viscosity variations for sucrose solutions, are somewhat different in magnitude when polyacrylamide is added. Within Fig. 4, data are included for 80 ppm and 100 ppm polymer solutions for a fluid temperature of 20^oC. Here, polymer solution viscosities also do not vary substantially with shear rate, with values which are often larger than the pure sucrose solution values for 0 ppm, when compared at the same fluid temperature and shear rate. As such, viscosity magnitudes from the present study are generally consistent with values given by Abed et al. [9].

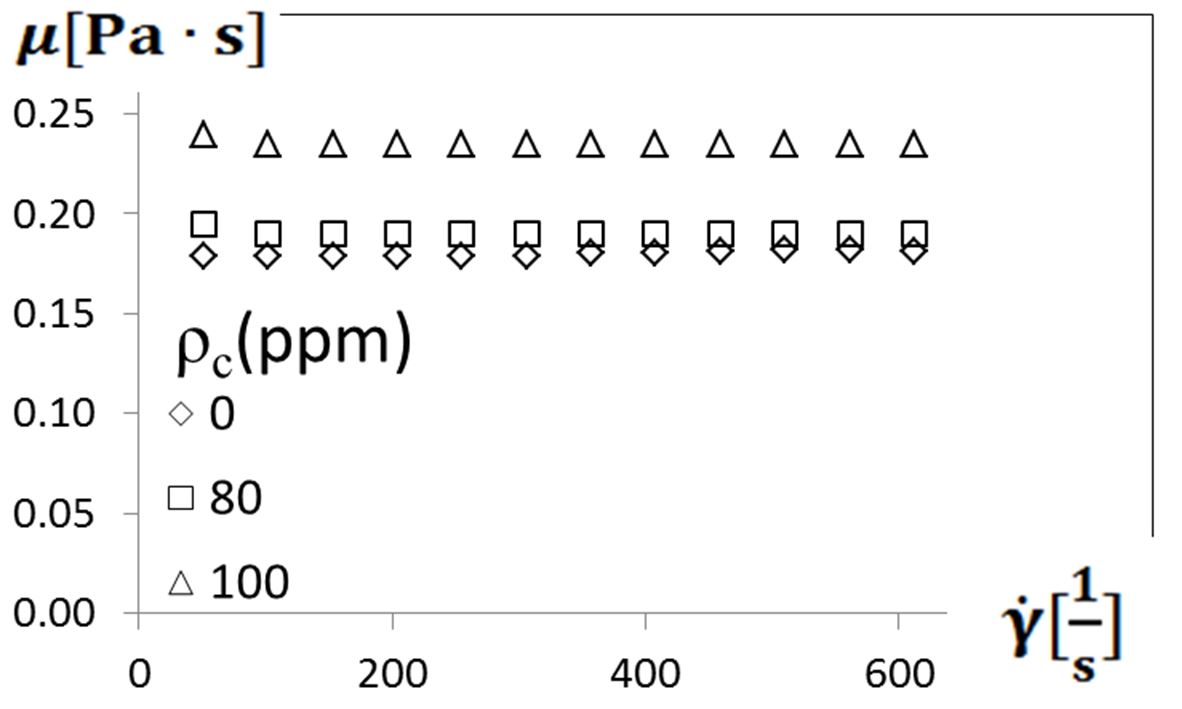
Figure 4. Viscosity variations with shear rate for different polymer concentrations for a fluid temperature of 20^oC.

C. Visualizations of Flow Characteristics

Flow visualization images for sucrose and 100 ppm polymer solution are presented in Fig. 5, with a flow passage height of 640 µm. Visualization images in Fig. 5a are shown for a range of rotation speeds for the sucrose solution from 100 RPM or 10.47 radians/sec. to 1000 RPM or 104.7 radians/sec., and shear rates from 29.21 1/s to 292.1 1/s. Visualization images in Fig. 5b are shown for 100 ppm viscoelastic polyacrylamide solution at the same rotation speeds and shear rates. As the dye is injected near the middle of the inlet flow passage, dye trajectories and distributions illustrate the mixing and agitation from the elastic turbulence. The pathlines as presented in Fig. 5a are smooth, narrow and well defined with little distortion as the rotation speed increases, following the trajectory of laminar flow streamlines. The pure laminar distribution of the dye indicates that only minimal secondary flow and no augmented mixing occurs within the channel.

When the 100 ppm polymer solution is employed, flow behavior, which is illustrated by the results in Fig. 5b, is dramatically different compared to the sucrose solution results. Images within Fig. 5b show that mixing is significantly enhanced, since dye begins to spread immediately at or near the inlet of the flow passage. In some cases, this spreading may occur initially within the flow passage near the VDP inlet. Afterwards, dye is spread throughout the entire flow passage, and over the entire radial extent of the passage. These events occur within flow geometries which produce significant streamline curvature, resulting in initial polymer agitation, as well as increased stretching in the circumferential direction. Because associated overall shear rates are 29.32 1/s or higher, the dramatic dye spreading is associated with the onset and development of elastic turbulence.

The differences in flow visualization images between Figs. 5a and 5b are not due to increased viscosity values alone, because the natural tendency of increased viscosity (with or without polymers present) is suppression of flow fluctuations. In addition, centrifugal instabilities associated with streamline curvature are not responsible for the observed variations, because associated Dean numbers are not large enough to allow development of the associated centrifugal-instability induced secondary flows. The experimental conditions associated with transition also cannot be characterized by one Dean number, and associated Dean numbers do not vary with polymer concentration. Within the present investigation, Reynolds numbers, based upon flow passage gap height and spatially-averaged velocity, range from 0.03 to 0.24. Reynolds numbers, based upon flow passage gap height and rotation speed at the flow passage centerline, range from 0.11 to 0.87. Because the radius of the convex surface is the same as the radial extent of the flow channel, associated Dean numbers cover the same range of values.

Figure 5. Flow visualization images. Sucrose solutions with (a) 0 ppm polyacrylamide concentration, and (b) 100 ppm polyacrylamide concentration.

Elastic turbulence is also induced by streamline curvature and the associated flow strain which is imposed on the flow as streamlines turn from the fluid inlet port into the C-shaped channel. Local secondary flows, small-scale vortical regions, and regions of augmented shear adjacent to small-scale flow separation zones, also probably contribute to locally augmented magnitudes of flow strain. Here, the formation of centrifugally-induced Dean vortex pairs is unlikely because streamwise curvature from the turn is not imposed over sufficient streamwise distance to induce the development of centrifugal instabilities [17,18,19]. However, even if such Dean vortex pairs were present (which they are not), they do not have sufficient magnitudes of local vortex circulation to produce the augmentations of local flow mixing and spatially-averaged Nusselt numbers which are observed within the VDP (and discussed later) [18,19]. As such, the only phenomenon present which can induce the observed variations is elastic turbulence.

Diffusion velocities provide information in regard to the transport of dye distributions associated with experimental data, such as are shown in Figs. 5a and 5b. Such velocities are presented in Fig. 6, as they vary with polymer concentration and viscous disk pump rotational speed. Here, dimensional diffusion velocities are given by the ratio of kinematic viscosity to flow passage gap height, or ν/s. As such, this parameter represents variations of transport only from molecular effects. Figure 6 shows that diffusion velocity values increase with polymer concentration for each value of disk rotational speed, and increase with rotational speed for each value of polymer concentration. For each value of disk rotational speed, minimum diffusion velocity is then always associated with the 0 ppm polymer concentration, for the associated Newtonian fluid.

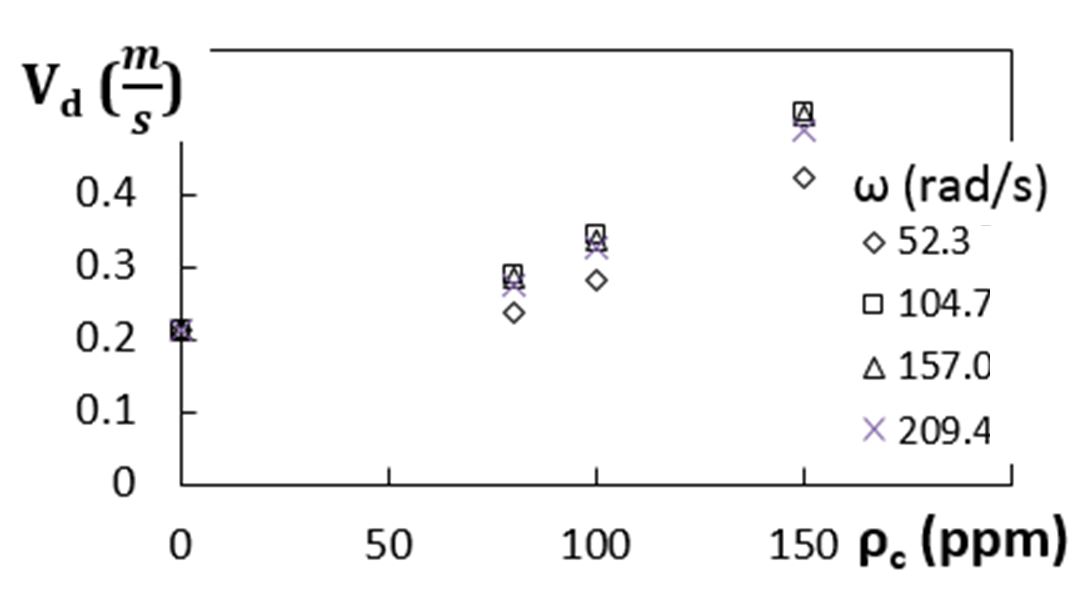
Figure 6. Diffusion velocity as it varies with polymer concentration and viscous disk pump rotational speed.

The observed increases of molecular transport diffusion velocity with polymer concentration and with disk rotational speed can help increase overall transport levels, but only by relatively small amounts. To counter such transport level increases, higher dimensional molecular-based diffusion velocities probably contribute to the suppression of the onset and development of elastic turbulence. This is because associated increases in absolute viscosity and kinematic viscosity generally suppress unsteady flow fluctuations and chaotic fluid motions, relative to Newtonian fluids, where viscosity values are lower.

D. Flow Conditions For Transition to Elastic Turbulence

     The experimental conditions for transition to elastic turbulence for different polymer concentrations and different shear rates at 20^oC are given in Figure 7. These transition data are determined from visualization images at a gap height of 640 μm, when the disk rotational speed Ω is between 100 RPM (or 10.47 radians/s) and 2000 RPM (or 209.4 radians/s). Associated shear rates are 29.21 1/s and 584.2 1/s, respectively. The transition onset is evidenced as dye becomes more spread out and more diffuse throughout the viscous disk pump flow passage, as shown in Fig. 5. Figure 7 shows that this transition onset occurs at lower shear rates as the concentration of polyacrylamide increases. This is attributed to coil stretch transition phenomena, and increased interactions between the polymer chains within the flow, as polymers per unit volume become more numerous.

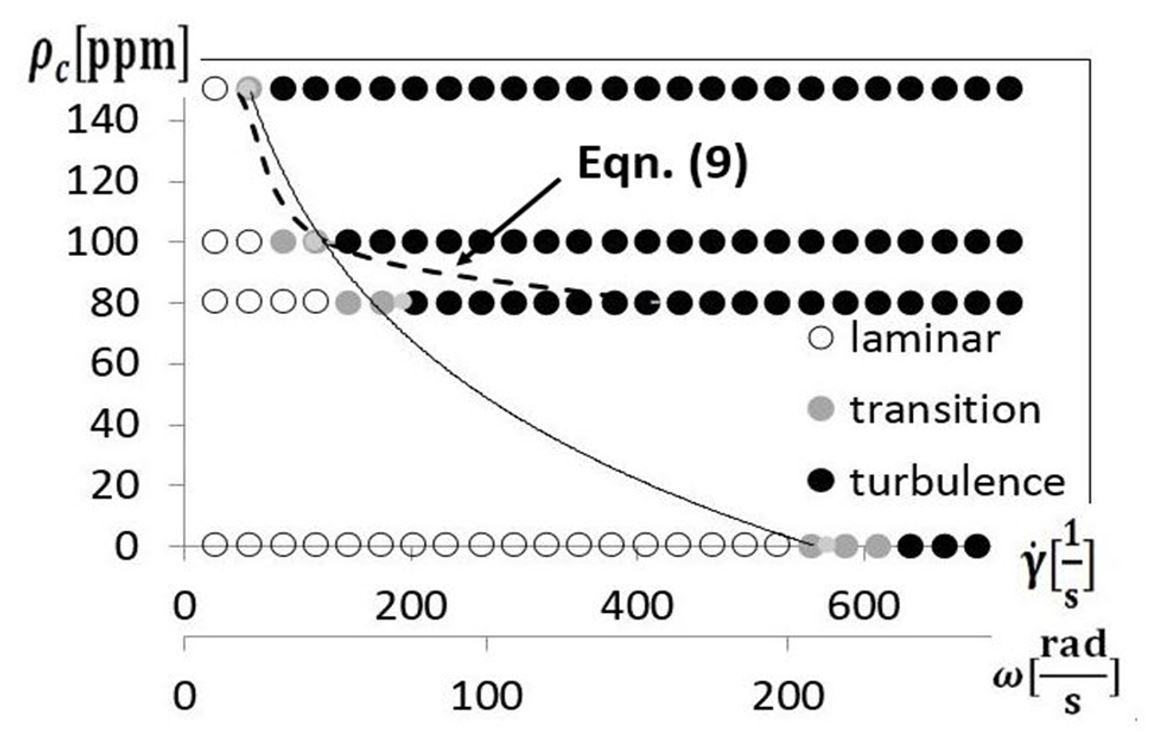
Figure 7. Transition onset within the viscous disk pump from flow visualization images.

Note that the changes illustrated by the data in Fig. 7 cannot be attributed to secondary flows from centrifugal instabilities. This is because the experimental conditions associated with transition cannot be characterized by one Dean number, and because associated centrifugal instabilities (and associated Dean numbers) do not vary with polymer concentration.  In addition, sufficient streamwise development length is not provided to induce the development of Dean vortex pairs, for the curved streamlines which are present as flow advects from the inlet port to the C-shaped channel, as mentioned earlier.

According to Burghelea et al. [21], the microscopic phenomenon responsible for macroscopic elastic turbulence flow is called “coil-stretch transition”. This occurs when the polymer molecules are strongly stretched to sizes which approximate the total polymer length. This occurs when the stretch rate exceeds the inverse polymer relation time. This stretch rate condition is then also the basis of the definition of the Weissenberg number. When greater than some threshold value, higher Wi values, and sufficiently high stretch rates, then evidence the onset and presence of elastic turbulence. Timewise variations of a fluid with long polymer molecules are thus important because the polymers allow the fluid to store stresses. This storage capability gives the fluid a memory, which makes them non-Newtonian. Within curvilinear shear flows, the overall result is complicated and irregular local fluid motions. Additional consequences include polymer feedback to and from the surrounding flow. This leads to non-uniform distributions of elastic stresses, and additional polymer stretching, as well as enhanced development of strongly non-linear, non-Newtonian flow behavior [21].

Note that, when the stretching rate of the flow is smaller than the inverse polymer relaxation time, deformation of the polymers is moderate. With this situation, the polymer solution flows are closer to Newtonian, with no memory. As a result, the influence of polymers on the flow is negligible.

E. Variations of Overall Pressure Rise and Shear Stress

Variations of dimensional pressure rise with dimensional volumetric flow rate (and dimensional mass flow rate) are illustrated by the data given in Fig. 8 for a rotation speed of 2000 RPM (or 209.4 radians/s), and a shear rate of 584.2 1/s. Here, dimensional pressure generally decreases with dimensional mass (or volume) flow rate in an approximately linear fashion, for the sucrose solution, as well as for the 100 ppm polymer solution. As a result, the maximum dimensional pressure rise is obtained for zero volumetric flow rate (for each polymer concentration). When compared at the same mass flow rate, volumetric flow rate, shear rate, and disk rotational speed, Fig. 8 shows that dimensional pressure drop is significantly larger for the viscoelastic fluids, with larger slope variation as mass flow rate varies, relative to the Newtonian solutions. Here, the decrease of static pressure rise with increasing flow rate indicates that the present VDP behaves similarly to a radial flow pump with backward curved impeller blades.

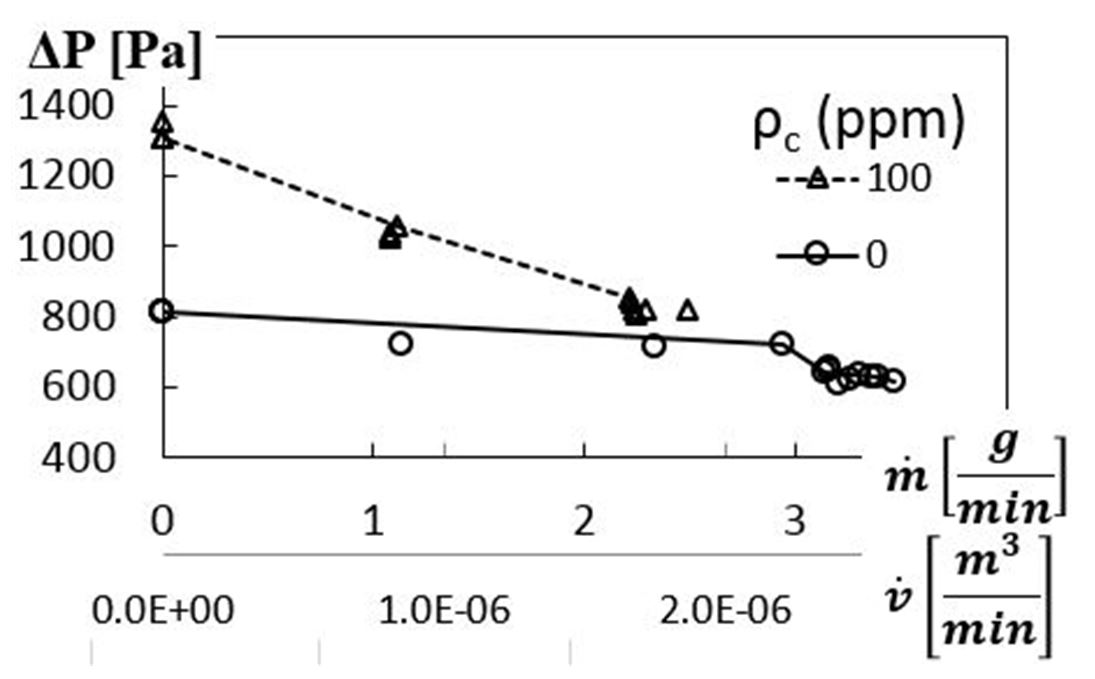
Figure 8. Dimensional pressure rise variations with dimensional mass and volumetric flow rates.

The relationship between dimensional pressure rise and overall dimensional shear stress within the viscous disk pump is given for the sucrose solution, as well as for the 100 ppm polymer solution, in Fig. 9. These data are also provided for a rotation speed of 2000 RPM (or 209.4 radians/s), a shear rate of 584.2 1/s, and a flow passage height of 640 μm. All data show that pressure rise increases as dimensional shear stress increases, regardless of the type of fluid. In general, higher magnitudes of overall shear stress and pressure rise are present for the combination polymer/sucrose solutions, relative to the sucrose only solutions, with data for both solutions approximately following similar trend.

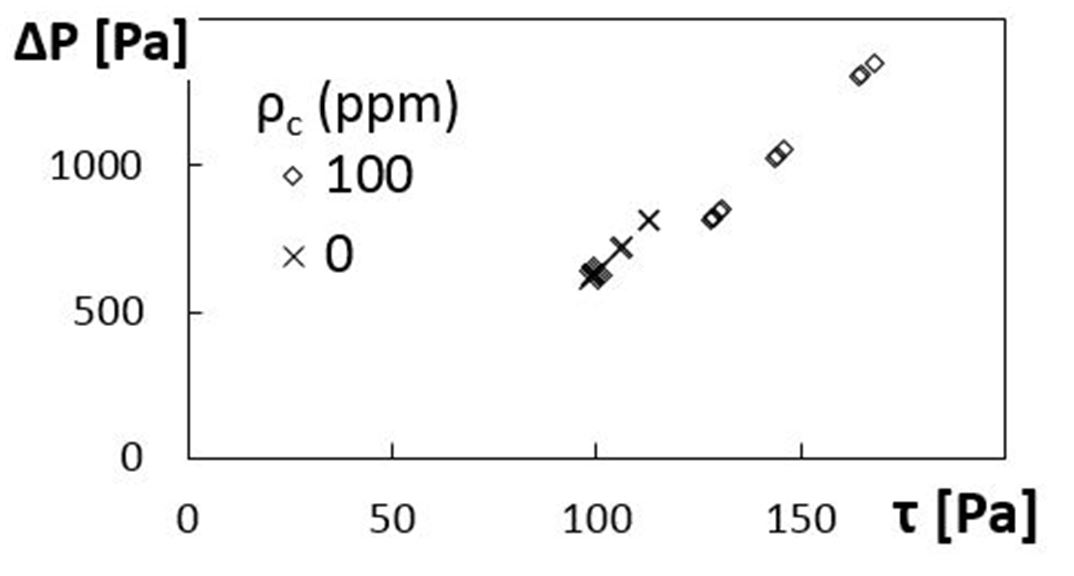
Figure 9. Dimensional pressure rise variations with dimensional overall shear stress.

Larger elastic turbulence effects are generally associated with larger magnitudes of local and spatially-averaged shear stress. Figs. 8 and 9 indicate the most important polymer agitations associated with elastic turbulence generally occur as the dimensional volumetric flow rate becomes smaller. As such, the present data show that polymer solutions can cause sharp growth in flow resistance, as elastic turbulence develops. As a result, secondary flow develop in the viscoelastic flow due to the normal stresses, which are tied to streamline curvature within the C-shaped channel, leading to the onset and development of elastic turbulence [10]. According to Burghelea et al. [21], the mixing and secondary flows associated with elastic turbulence are driven by the “coupling” between the primary circumferential shear flow and the secondary radial polymer elongation flow. This “coupling” between radial and shear flows within the VDP then leads to increased polymer stretching in the circumferential direction, increased polymer agitation, higher shear stresses, and larger static pressure rises.

Associated values of overall shear stress, are given in Fig. 10 as they vary with dimensional mass and volumetric flow rates. These data are provided for the same experimental conditions as the data in Figs. 8 and 9. Here, for each polymer concentration (0 ppm and 100 ppm), overall shear stress declines (approximately) linearly with dimensional volumetric (and mass) flow rate. Here, shear stress values include contributions from both Couette flow and Poiseuille flow, which depend separately, and respectively, upon shear rate and pressure rise. Overall, the results in Figs. 8, 9, and 10 show that the largest polymer agitations associated with elastic turbulence occur at higher pressure rises, higher shear stress values, and lower volumetric flow rates within the viscous disk pump.

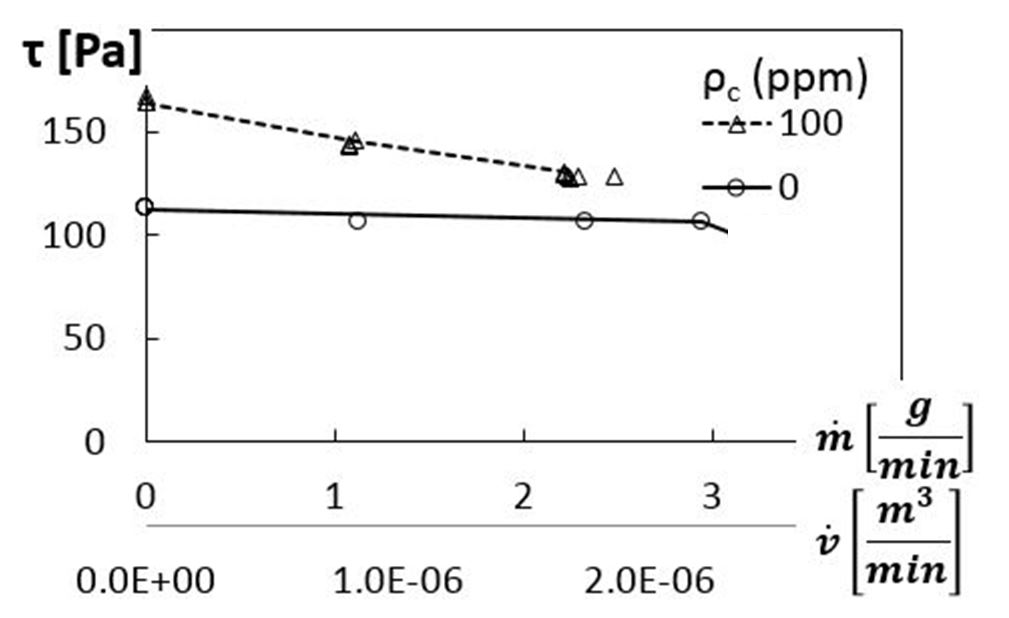
Figure 10. Dimensional overall shear stress variations with dimensional mass and volumetric flow rates.

F. Convective Heat Transfer Characteristics

Variations of convective heat transfer characteristics for the polyacrylamide/sucrose solutions and the Newtonian solutions are determined from measurements and analysis, and are given in Figs. 11 and 12. Results are given for disk rotational speeds of 500 RPM, 1000 RPM, 1500 RPM, and 2000 RPM, or 52.3 radians/s, 104.7 radians/s, 157.1 radians/s, and 209.4 radians/s, respectively, with respective overall shear rates of 146.0 1/s, 292.1 1/s, 438.1 1/s and 584.2 1/s

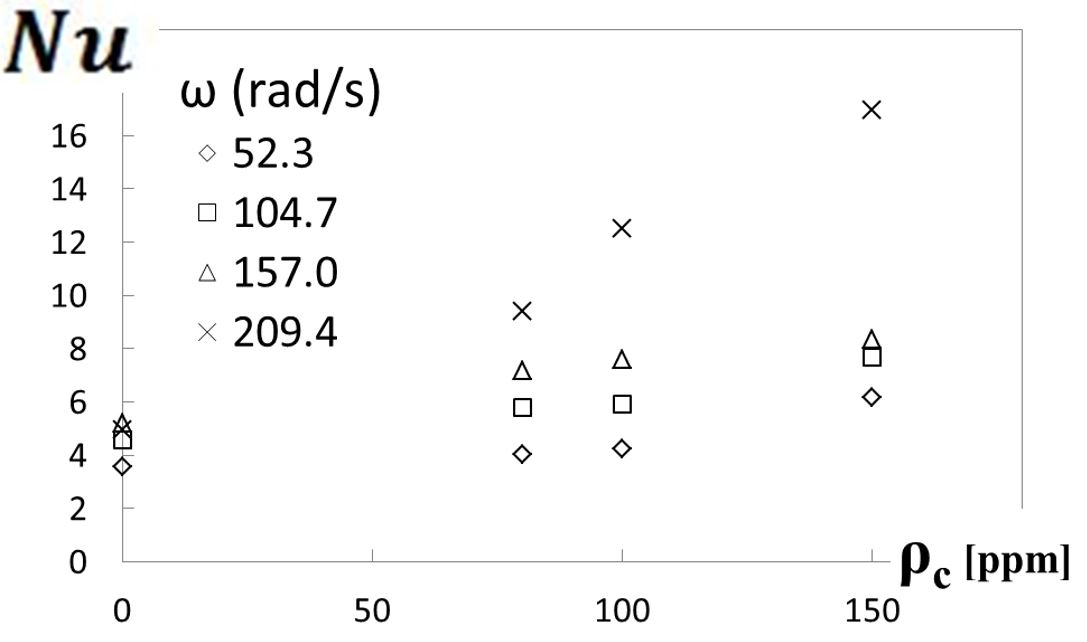
Figure 11. Overall Nusselt number variations with polymer concentration for different viscous disk pump rotational speeds.

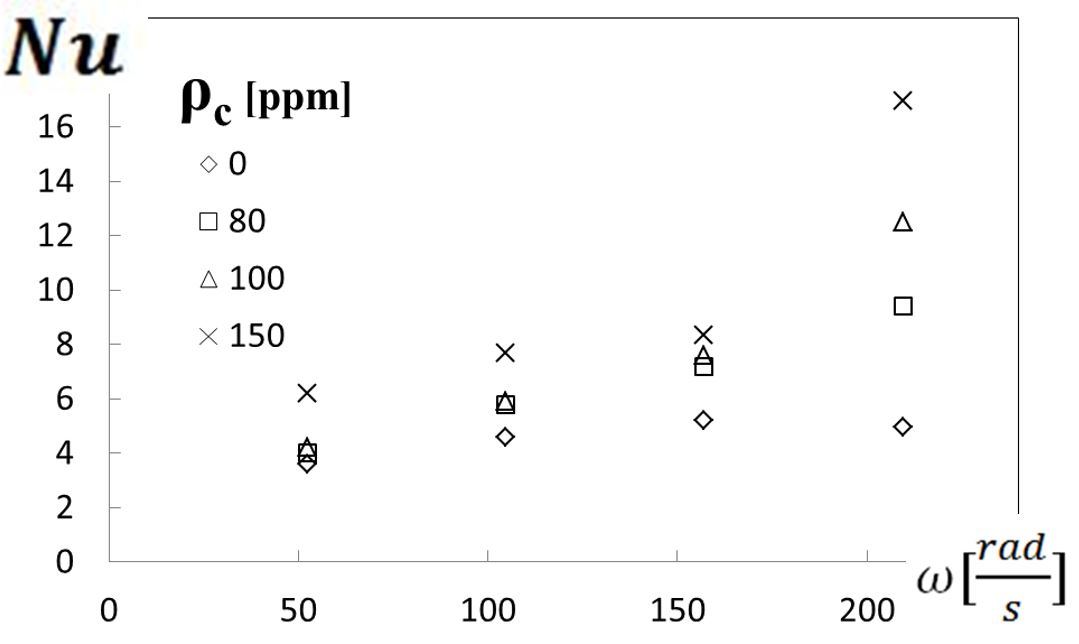
Figure 12. Overall Nusselt number variations with viscous disk pump rotational speed for different polymer concentrations.

Figure 11 shows that spatially-averaged Nusselt numbers increase with increasing polymer concentration for each of the four shear rates considered (and for each of the four disk rotational speeds). Figure 12 then shows that spatially-averaged Nusselt numbers increase with disk rotational speed for each polymer concentration employed. When compared for a particular shear rate or disk rotation speed, the minimum Nusselt number is always associated with the 0 ppm sucrose solution. Spatially-averaged Nusselt numbers thus show significant variations as polyacrylamide concentration is changed, which are tied to different extents of elastic turbulence development. Associated variations within the viscous disk pump flow passage are thus associated with increased polymer interactions and agitation, and enhanced local mixing, which results in overall increases in local and global thermal transport.

As such, the elastic turbulence increases heat transfer by approximately 240 percent for the sucrose solution with a 150 ppm polymer concentration (relative to the Newtonian solution with ρ_c=0 ppm, when compared at the same disk rotational speed). Abed et al. [9] describe enhancements as large as 380 percent for sucrose solutions with 500 ppm polymer concentrations. Those investigators attribute such enhancements to the elastic turbulence generated by non-linear interactions between elastic normal stresses created within the flowing high-molecular-weight polymer solution, and the streamline curvature of a serpentine channel.

G. Variations of Mean-Square of Temperature Fluctuations

Such increased mixing, and increased polymer interactions and agitation from elastic turbulence are illustrated by variations of mean square magnitudes of flow temperature fluctuations (measured at the viscous disk pump passage exit). These data are given in Figs. 13 and 14. Within Fig. 13, these data are given as they vary with polymer concentration for rotational speeds Ω of 500 RPM, 1000 RPM, 1500 RPM, and 2000 RPM (or 52.36 radians/s, 104.7 radians/s, 157.1 radians/s, and 209.4 radians/s), and respective shear rates of 146.0 1/s, 292.1 1/s, 438.1 1/s, and 584.2 1/s. Figure 14 then presents data as they vary with disk rotational speed for the viscous disk pump for polymer concentrations of 0 ppm, 80 ppm, 100 ppm, and 150 ppm. As such, unsteady temperature fluctuations offer an appropriate means to characterize flow mixing and small-scale interactions because, like dye concentrations, temperature is a passive scalar. Consequently, both quantities are influenced by similar advection and diffusion transport phenomena.

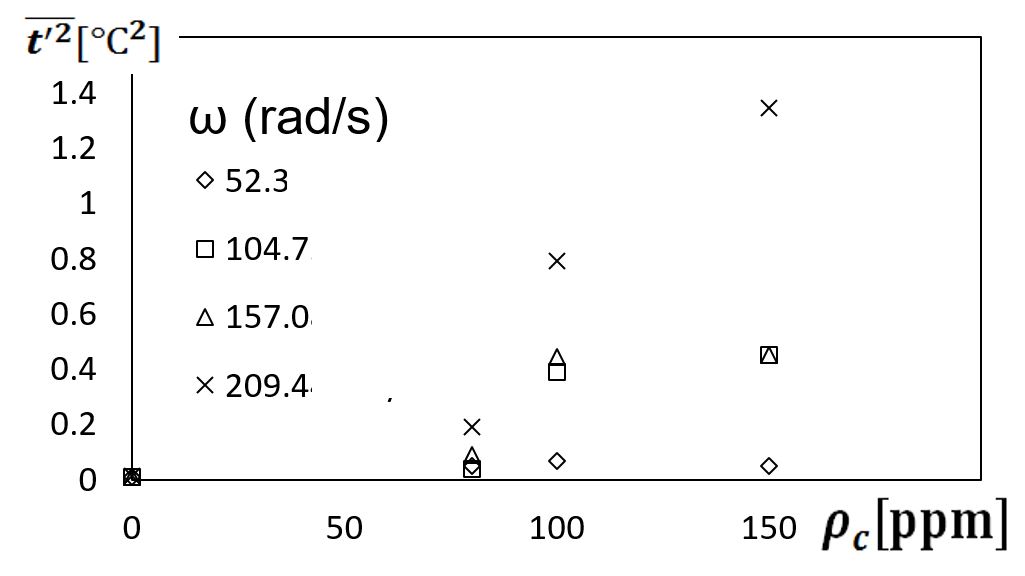
Figure 13. Variations of mean-square magnitudes of flow temperature fluctuations with polymer concentration for different viscous disk pump rotational speeds.

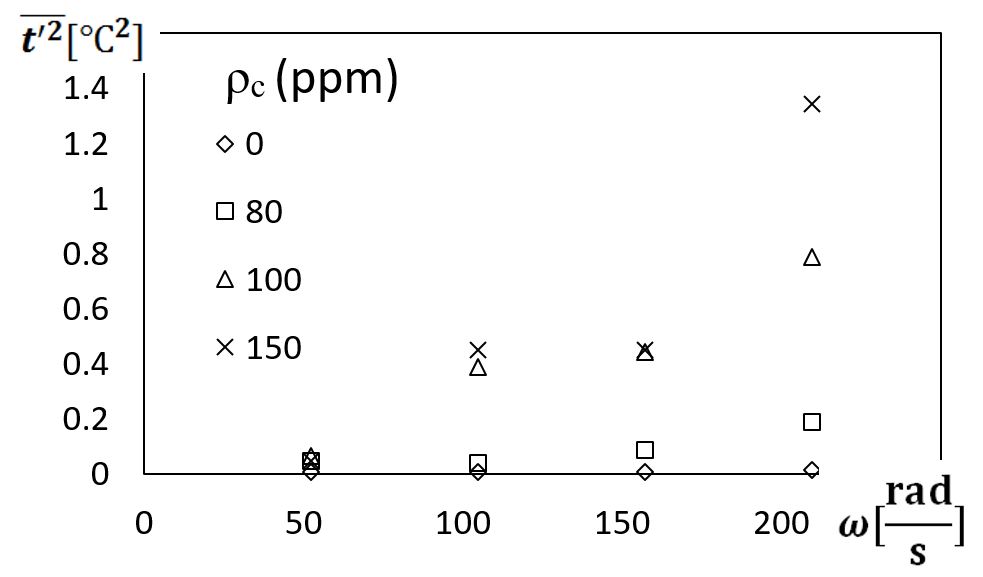
Figure 14.  Variations of mean-square magnitudes of flow temperature fluctuations with viscous disk pump rotational speed for different polymer concentrations.

Dramatic $latex \bar { t’ } ^{ 2 }&bg=d3dce6&s=-3$ increases are evident in Fig. 13 as polymer concentration increases, especially for disk rotation speeds greater than 100 radians/s. These changes to $latex \bar { t’ } ^{ 2 }&bg=d3dce6&s=-3$ with ω and ρ_c are further confirmed by the results which are presented in Fig. 14. Regardless of the rotational speed of the disk, and the associated shear rate, the lowest dimensional magnitudes of $latex \bar { t’ } ^{ 2 }&bg=d3dce6&s=-3$ are always associated with the Newtonian fluid, wherein ρ_c=0 ppm. As such, the changes resulting from increasing ω and ρ_c are associated with increased flow irregularities and unsteadiness, which result from polymer twisting, convolutions, and interactions. As such, the present $latex \bar { t’ } ^{ 2 }&bg=d3dce6&s=-3$ data illustrate local chaotic fluid motions associated with the onset and development of elastic turbulence.

H. Power Spectra of Fluctuating Temperature

The frequency content of the unsteady temperature fluctuations is illustrated by the results in Fig. 15. These data are given for a rotational speed Ω of 1500 RPM (or 157.1 radians/s), a shear rate of 438.1 1/s, and for different polymer concentrations. Included is one data set for a Newtonian fluid, wherein ρ_c=0 ppm. From these data, it is evident that the polymer solutions exhibit higher spectral magnitudes over broad-band frequencies. In addition, wider and more pronounced spectral peaks are present at different frequencies, especially in the vicinity of 10^-1 Hz. The dramatic differences in the power spectra between polymer solutions and Newtonian solution are caused by flow fluctuations over a range of frequencies resulting from elastic turbulence. Also important is the suppression of flow fluctuations from increased viscosity (with no polymers present) associated with the Newtonian fluid.

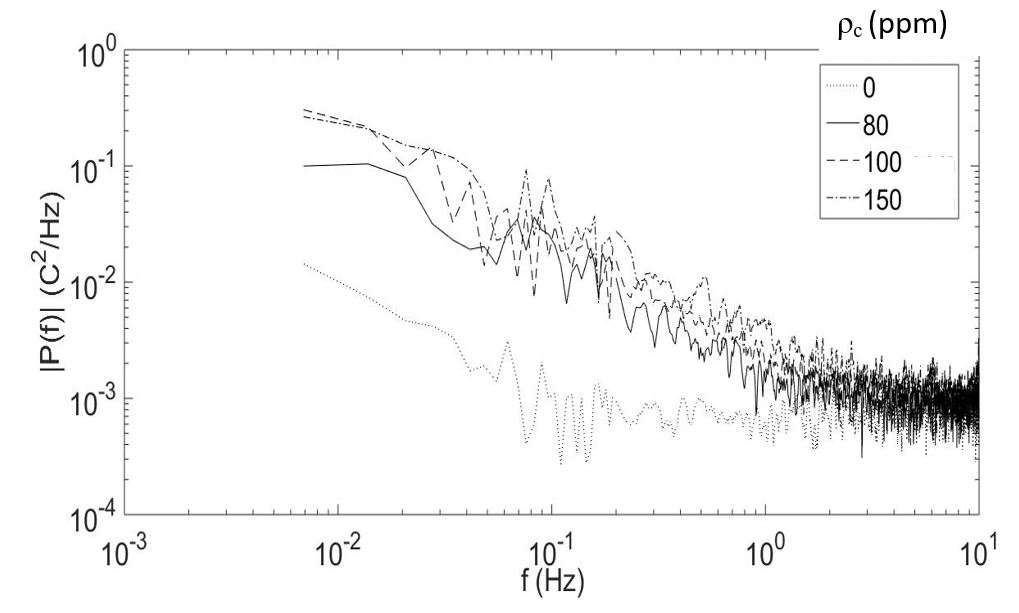
Figure 15. Power spectra of temperature fluctuations as they vary with polymer concentration.

IX. Conclusions

Elastic turbulence is employed within the present investigation to enhance convective heat transfer at very small scales and at very low Reynolds numbers. A miniature viscous disk pump or VDP is utilized to investigate flow and heat transfer characteristics, where the latter are based upon energy balance measurements which utilize the mixed-mean temperature at the inlet and outlet of the VDP flow passage. The overall heat transfer rate is determined based upon a constant surface temperature thermal boundary condition, and upon a log-mean-temperature difference approach. The VDP operates at rotation speeds of 500 RPM, 1000 RPM, 1500 RPM, 1800 RPM, and 2000 RPM (or 52.36 radians/s, 104.7 radians/s, 157.1 radians/s, 188.5 radians/s, and 209.4 radians/s, respectively), which produce overall shear rates across the flow cross section of 146.05 1/s, 292.1 1/s, 438.1 1/s, 525.8 1/s, and 584.2 1/s. A channel depth of 640 µm is employed. Elastic turbulence is induced by adding polyacrylamide to water solutions with 65 % sucrose by mass.

Significant enhancements of mixing and transport are observed, which are associated with the onset and development of elastic turbulence. Such behavior is verified, relative to Newtonian fluid solvents, using flow visualization results, pressure rise data, overall shear stress variations, increases of overall magnitudes of convective Nusselt numbers, increases of time-averaged magnitudes of mean-square temperature fluctuations, and increases of spectral energy content of unsteady temperature fluctuations. Note that the enhancements observed are not due to increased viscosity values alone, because the natural tendency of increased viscosity (with or without polymers present) is suppression of flow fluctuations and local chaotic fluid motions. Increases of viscosity values associated with the polymer solutions, relative to Newtonian solvents, are not sufficient to induce the observed Nusselt number augmentations (even though such increases result in enhanced molecular transport). In addition, centrifugal instabilities associated with streamline curvature are not responsible for the observed variations, because associated Dean numbers are not large enough, or the streamwise extent of streamline curvature is not extensive enough, to allow development of the associated centrifugal-instability induced secondary flows. In addition, the experimental conditions associated with elastic turbulence transition cannot be characterized by one Dean number, and associated centrifugal instabilities (and associated Dean numbers) do not vary with polymer concentration.

Within the present investigation, the elastic turbulence increases heat transfer by as much as 240 percent for the sucrose solution with a 100 ppm polymer concentration (relative to the Newtonian solution with ρ_c=0 ppm, when compared at the same disk rotational speed). Dramatic $latex \bar { t’ } ^{ 2 }&bg=d3dce6&s=-3$ increases are also evident as polymer concentration increases, especially for disk rotation speeds greater than 100 radians/s. Regardless of the rotational speed of the disk and the associated shear rate, the lowest dimensional magnitudes of $latex \bar { t’ } ^{ 2 }&bg=d3dce6&s=-3$ are always associated with the Newtonian fluid, wherein ρ_c=0 ppm. As such, the changes resulting from increasing ω and ρ_c are associated with increased flow irregularities and unsteadiness, which result from coil-stretch transition development of elastic turbulence, with the associated polymer twisting, convolutions, and interactions. Such trends in regard to the onset and development of elastic turbulence are consistent with flow visualization results, and variations of static pressure rise and overall shear stress.

Acknowledgements

The research described in this paper is supported by the U.S. National Science Foundation, Grant No. CBET-1501587. The Anton Paar Corporation is acknowledged for loaning a commercial Anton Paar Rheometer MCR 302 to the University of Alabama in Huntsville for use during the present investigation. Mr. Benjamin Lund is acknowledged for his contributions to the development of the experimental facility employed within the present investigation.

References

[1] De Gennes, P. G., “Coil‐Stretch Transition of Dilute Flexible Polymers Under Ultrahigh Velocity Gradients,” Journal of Chemical Physics, Vol. 60, No. 12, 1974, pp. 5030 to 5042.

[2] Naschie, M. S. E., Athel, S. A., and Kapitaniak, T., “A Note on Elastic Turbulence and Diffusion,” Journal of Sound and Vibration, Vol. 155, No. 3, 1992, pp. 515-522.

[3] Berti, S., and Boffetta, G., “Elastic Waves and Transition to Elastic Turbulence in a Two-Dimensional Viscoelastic Kolmogorov Flow,” Physical Review E, Vol. 82, 2010, pp. 036314-1 to 036314-8.

[4] Berti, S., Bistagnino, A., Boffetta, G., Celani, A., and Musacchio, S., “Two-Dimensional Elastic Turbulence,” Physical Review E, Vol. 77, 2008, pp. 055306-1 to 055306-4.

[5] Schiamberg, B. A., Shereda, L. T., Hu, H., and Larson, R. G, “Transitional Pathway to Elastic Turbulence in Torsional, Parallel-Plate Flow of a Polymer Solution,” Journal of Fluid Mechanics, Vol. 554, 2006, pp. 191-216.

[6] Li, F.-C., Kinoshita, H., Li, X.-B., Oishi, M., Fujii, T., and Oshima, M, “Creation of Very-Low-Reynolds-Number Chaotic Fluid Motions in Microchannels Using Viscoelastic Surfactant Solution,” Experimental Thermal and Fluid Science, Vol. 34, No. 1, 2010, pp. 20-27.

[7] Hartnett, J. P., and Kostic, M, “Heat Transfer to a Viscoelastic Fluid in Laminar Flow Through a Rectangular Channel,” International Journal of Heat and Mass Transfer, Vol. 28, 1985, pp. 1147-1155.

[8] Hartnett, J. P, “Viscoelastic Fluids: A New Challenge in Heat Transfer,” ASME Transactions – Journal of Heat Transfer, Vol. 14, 1992, pp. 296-303.

[9] Abed, W. M., Whalley, R. D., Dennis, D. J. C., and Poole, R. J, “Experimental Investigation of the Impact of Elastic Turbulence on Heat Transfer in a Serpentine Channel,” Journal of Non-Newtonian Fluid Mechanics, Vol. 231, 2016, pp. 68-78.

[10] Whalley, R. D., Abed, W. M., Dennis, D. J. C., and Poole, R. J, “Enhancing Heat Transfer at the Micro-Scale Using Elastic Turbulence,” Theoretical and Applied Mechanics Letters, Vol. 5, 2015, pp. 103-106.

[11] Traore, B., Castelain, C., and Burghelea, T, “Efficient Heat Transfer in a Regime of Elastic Turbulence,” Journal of Non-Newtonian Fluid Mechanics, Vol. 223, 2015, pp. 62-76.

[12] Zhang, H. N., Kunugi, T., Li, F. C., and Yu, B, “DNS Study of the Elastic Turbulence in a 3D Parallel Plate Channel,” Fourteenth European Turbulence Conference, ENS, Lyon, France, 2013.

[13] Zhang, H. N., Li, F. C., Cao, Y., Kunugi, T., and Yu, B, “Direct Numerical Simulation of Elastic Turbulence and Its Mixing-Enhancement Effect in a Straight Channel,” Chinese Physics B, Vol. 22, No. 2, 2013, pp. 024703-1 to 024703-10.

[14] Ligrani, P. M., Jiang, H., Lund, B., and Jin, J. S., “Deviations Due to Non-Newtonian Influences Within a Miniature Viscous Disk Pump,” ASME Transactions-Journal of Fluids Engineering, Vol. 135, No. 3, 2013, pp. 031205-1 to 031205-12.

[15] Blanchard, D., Ligrani, P. M., and Gale, B., “Miniature Single-Disk Viscous Pump (Single-DVP), Performance Characterization,” ASME Transactions – Journal of Fluids Engineering, Vol. 128, No. 3, 2006, pp. 602-610.

[16] James, D. F., “Boger Fluids,” Annual Review of Fluid Mechanics, Vol. 41, 2009, pp. 129-142.

[17] Ligrani, P. M.., Niver, R. D., “Flow Visualization of Dean Vortices in a Curved Channel with 40 to 1 Aspect Ratio,”  Physics of Fluids, Vol. 31, No. 12, 1988, pp. 3605-3617.

[18] Ligrani, P. M., Choi, S., Schallert, A. R., Skogerboe, P., “Effects of Dean Vortex Pairs on Surface Heat Transfer in Curved Channel Flow,” International Journal of Heat and Mass Transfer, Vol. 39, No. 1, 1996, pp. 27-37.

[19] Ligrani, P. M., Hedlund, C. R., “Experimental Surface Heat Transfer and Flow Structure in a Curved Channel With Laminar, Transitional, and Turbulent Flows,” ASME Transactions-Journal of Turbomachinery, Vol. 126, No. 3, 2004, pp. 414-423.

[20] McKinley, G. H., Pakdel, P., Oztekin, A., “Rheological and Geometric Scaling of Purely Elastic Flow Instabilities,” Journal of Non-Newtonian Fluid Mechanics, Vol. 67, 1996, pp. 19-47.

[21] Burghelea, T., Segre, E., and Steinberg, V., “Elastic Turbulence in Von Karman Swirling Flow Between Two Disks,” Physics of Fluids, Vol. 19, 2007, pp. 053104-1 to 053104-26.