Buoyancy-Driven Continuous SPLITT Fractionation: A New Technique for Separation of Microspheres

RESEARCH AREAS

– Dimple Array on Surfaces of Channels
– Investigations of Confined, Millimeter-Scale, Unsteady Laminar Impinging Slot Jets
– Aerodynamic Losses and Mixing Losses from Turbine Airfoils
– Impingement Cooling
– Internal Cooling – Surface Heat Transfer Augmentation
– Miniature and Micro-Scale Pumps
– Surface Roughness
– Electronics Cooling
– Transitional Flows in Curved Channels
– Film Cooling
– Flow and Heat Transfer on and Near a Transonic Turbine Blade Tip
– Slip Phenomina in Micro-Fluidic Devices
– Buoyancy-Driven Continuous SPLITT Fractionation: A New Technique for Separation of Microspheres
– Investigations of Full-Coverage Film Cooling
– Shock Wave Boundary Layer Interactions
– Double Wall Cooling
– Elastic Turbulence
– Surface Roughness Effects on Impingement Jet Array Surface Heat Transfer
– Dean Flow Dynamics in Low-Aspect Ratio Spiral Microchannels

Buoyancy-Driven Continuous SPLITT Fractionation: A New Technique for Separation of Microspheres (J. Storey, P. Douglas, P. M. Ligrani, and K. M. Morten), Separation Science and Technology, Vol. 44, No. 9, pp. 1895-1922, January 2009. DOWNLOAD COPY OF PAPER

FIGURES

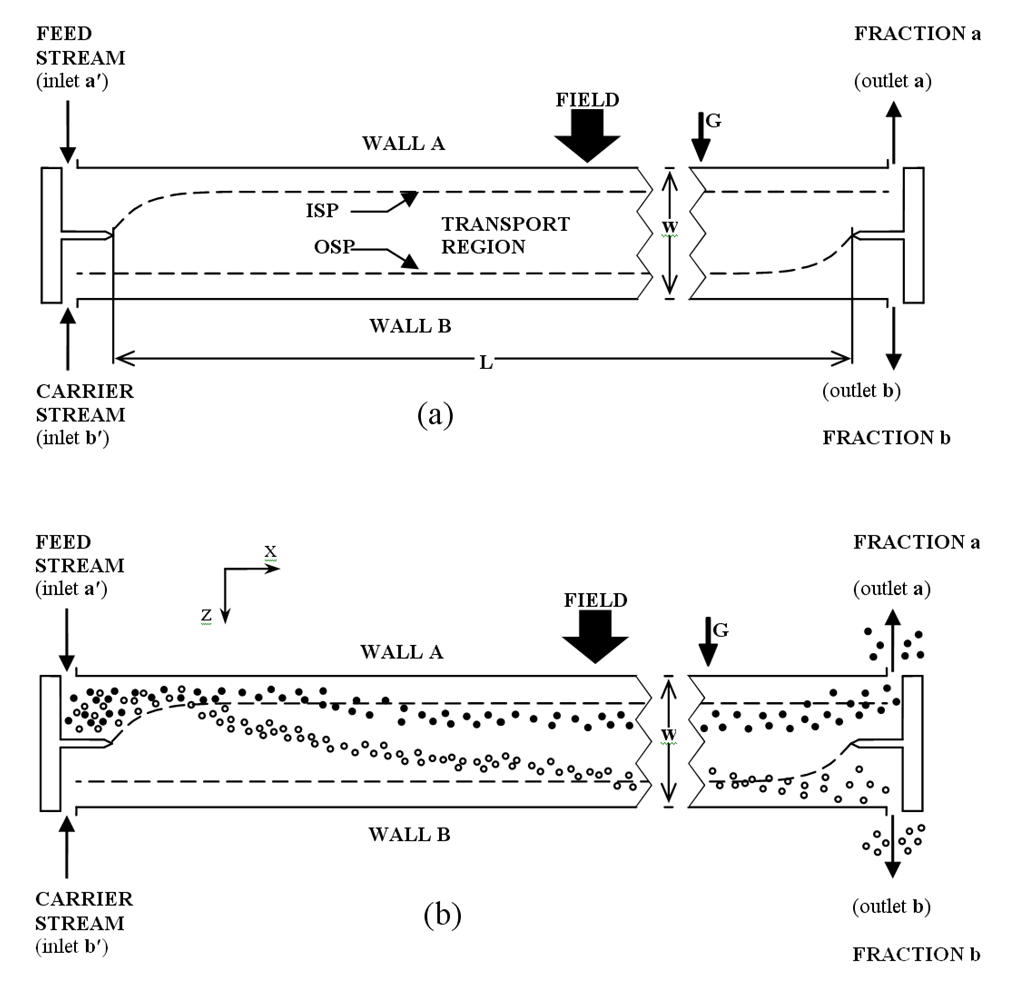Schematic view of a SPLITT cell operating in sedimentation transport mode, showing (a) the overall layout of the cell, and (b) example particle trajectories during operation.

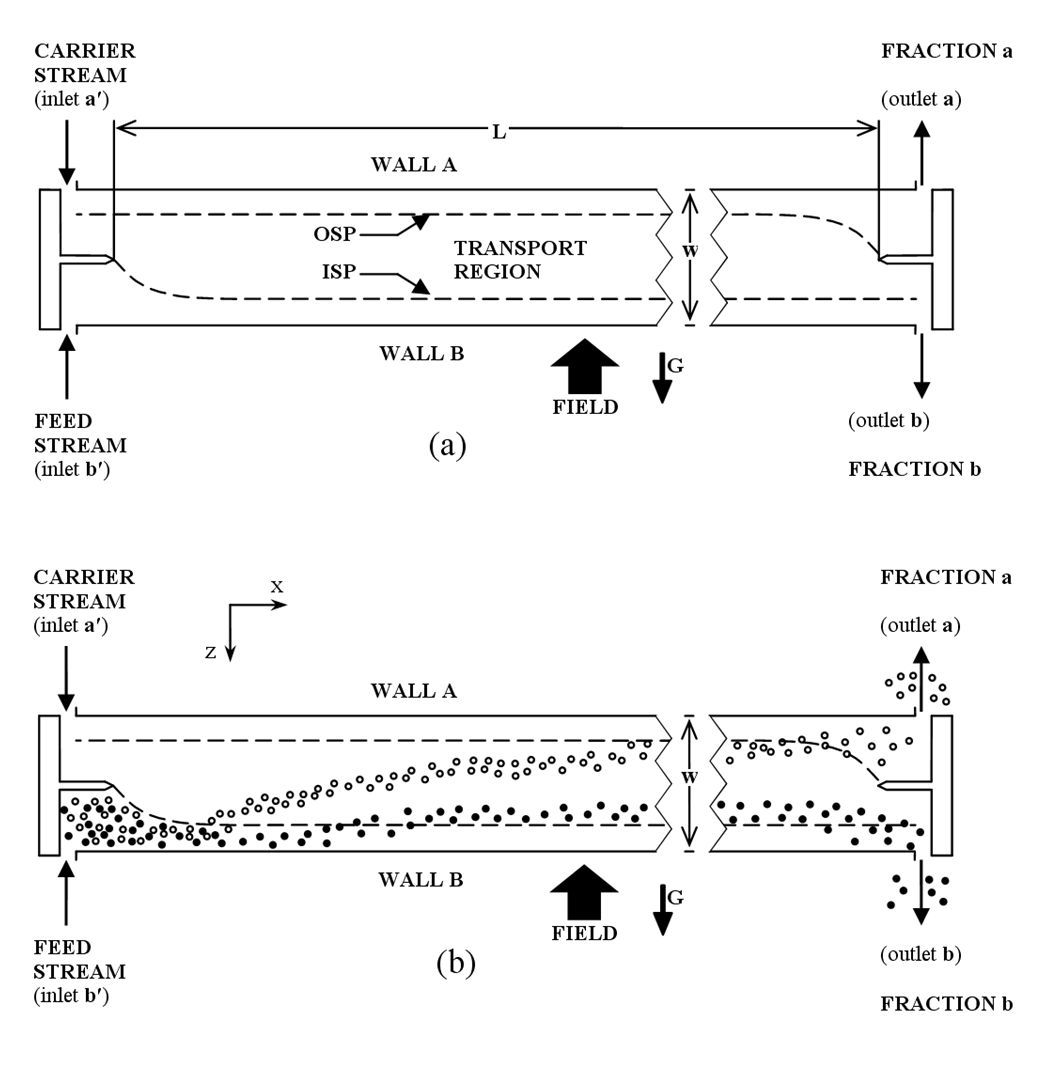Schematic view of a SPLITT cell operating in buoyancy-driven transport mode, showing (a) the overall layout of the cell and (b) example particle trajectories during operation.

Photograph of the cell for the sedimentation-driven and buoyancy-driven experiments.

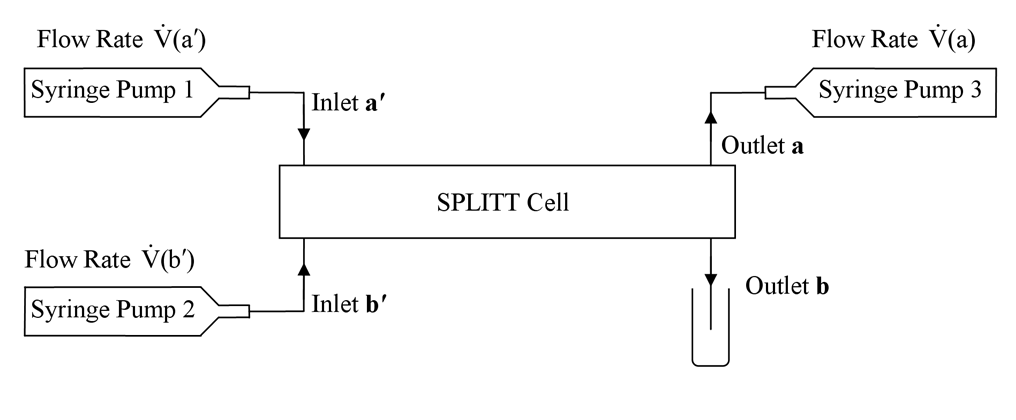
Schematic diagram showing flow connections to and from the cell, and the arrangement of the syringe pumps.

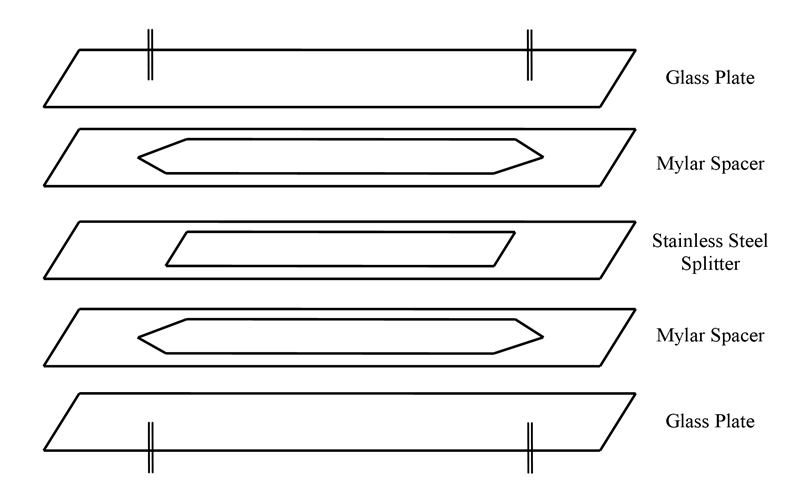Schematic diagram showing an overview of the cell construction and layout.